on&on
[Javascript] 최대공약수, 최소공배수는 유클리드 호제법으로! 본문
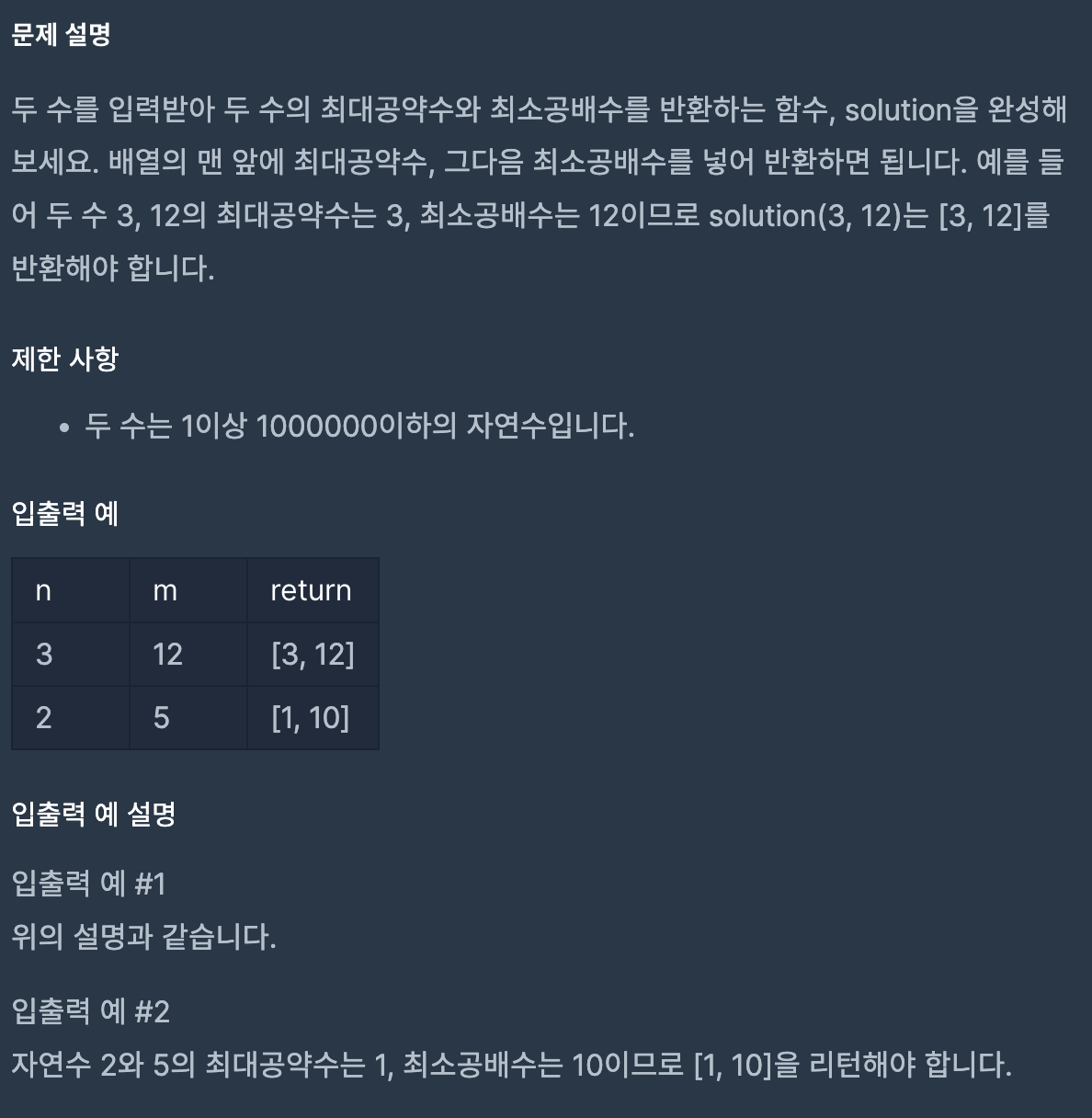
두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수 solution을 완성해보세요.
최대공약수
두 개 이상의 자연수의 공통된 약수 중 가장 큰 공약수
최소공배수
두 개 이상의 자연수의 공통된 배수 중 가장 작은 공배수
function solution(n, m, a, b) {
for(let i=1; i<=n; i++){
if(n%i===0 && m%i===0) a= i;
}
for(let i=1; i<=m*n; i++){
if(i%n===0 && i%m===0) {b = i; break;}
}
return [a, b]
}아무것도 고려하지 않고 풀은 어지러운 풀이
테스트 시간이 무려 30.61ms까지 나왔다...
다른 사람은 어떻게 봤는지 보다가 다음과 같은 풀이를 봤다.
function gcdlcm(a, b) {
var r;
for(var ab= a*b;r = a % b;a = b, b = r){}
return [b, ab/b];
}true/false 조건을 r=a%b로 판별하고, 0이 나오면 for문이 종료된다.
댓글을 보다가 '유클리드 호제법'이라는 것을 보고 궁금해져서 찾아보았다.
유클리드 호제법
두 자연수의 최대공약수를 구하는 알고리즘의 하나로 최대공약수를 구하는 알고리즘 중 가장 대표적인 알고리즘
호제법이란 두 수가 서로 상대방 수를 나누어서 원하는 수를 얻는 알고리즘
유클리드 호제법의 원리
1) 2개의 자연수가 a, b가 있다
2) a는 b보다 크다.
3) a를 b로 나눈 나머지는 r이다.
4) a, b의 최대공약수는 b, r의 최대공약수와 같다.
유클리드 호제법을 코드에 적용하면 다음과 같다.
// 삼항연산자 활용
function getGcd(a,b)
{
return b ? getGcd(b, a%b) : a;
}// while문 활용
function getGcd(a, b) {
while (b !== 0) {
n = a % b;
a = b;
b = n;
}
return a;
}최소공배수는 두 수를 곱해서 최대공약수로 나누면 구할 수 있다.
let gcd = getGcd(3, 6); // 최대공약수
let gcf = (3 * 6) / gcd; // 최소공배수유클리드 호제법을 활용해서 프로그래머스 문제를 풀어보면 시간 복잡도가 거의 반으로 줄어든 것을 볼 수 있다.
이해가 잘 안간다면 직접 하나씩 넣어보면서 이해하면 된다.
조금 이상하게 생겼지만 그래도 이렇게 혼자만의 방법으로 적다보면 최대공약수, 최소공배수 이해 완.
function getGcd(4,6)
{
return 6 ? getGcd(6, 4%6(4)){ // ⬆️ 2 반환
return 4? getGcd(4, 6%4(2){ // ⬆️ 2 반환
return 2 ? getGcd(2, 4%2(0){ // ⬆️ 2 반환
0 ? getGcd(0, 2%0) : 2 // ⬆️ 2 반환
}) : 4;
}) : 6;
}) : 4;
}'Javascript' 카테고리의 다른 글
| [Javascript] express로 proxy 서버 구축하고 CloudType에 배포하기 (0) | 2023.06.18 |
|---|---|
| [Javascript] 함수 레벨 스코프와 블록 레벨 스코프, 렉시컬 스코프 차이 이해하기 (0) | 2023.02.06 |
| [Javascript] Map을 활용한 최빈값 구하기 (0) | 2022.11.29 |
Comments



